La Tonique

Toute tonalité est construite autour d'une note principale : sa TONIQUE, également nommée « Ier degré » (car c'est la première note de la gamme choisie pour le morceau).

C'est elle qui "donne le ton" et détermine la tonalité, l'espace dans lequel se développera tout le morceau. C'est elle qui est précisée dans le titre de la pièce ("Ouverture en do mineur").

La tonique représente l'espace de repos absolu, d'où l'on part et où l'on revient.

C'est un peu comme la maison, que l'on quitte pour une promenade en montagne et, après des détours vers le haut et vers le bas, où l'on revient finalement se reposer.

Ou encore notre planète Terre, sur laquelle nous sommes basés, et depuis laquelle nous observons les autres planètes (les autres degrés).

C'est le point d'équilibre du système.

La Dominante

Vient ensuite le second personnage le plus important : la DOMINANTE, également appelée « Ve degré » (car c'est la 5ème note de la gamme choisie : par exemple, en do majeur, la dominante est sol).

C'est la dominante qui assure le rôle de « tension » maximale.

Là encore, il s'agit moins d'un son unique que d'un accord : par exemple, en do majeur, la dominante (le Ve degré) est l'accord parfait de sol (sol-si-ré).

De nombreuse raisons historiques et acoustiques expliquent tout cela. Gardons simplement à l'esprit que la tonalité est un système de tensions et de détentes, de suspensions et de repos, toujours en recherche d'équilibre.

Exemple

Voici un air bien connu : "Ah ! vous dirai-je maman".

1. Il démarre sur la tonique do ;
2. Puis s'accroche sur la dominante sol ("Papa"), comme "en suspension" ;
3. Pour conclure enfin en revenant sur do ("Moi") – note finale sur laquelle l'air se posera.

C'est ce parcours qui crée un "sentiment tonal".

« La plus ancienne date que je puisse citer pour Ah ! vous dirai-je, maman ? est 1740, puis les Folies de Coraline, pièce jouée en 1745 à la Comédie italienne. » J.-B. Weckerlin

... et les autres degrés

Viennent ensuite les autres degrés, plus ou moins importants, et qui apportent une sensation plus ou moins grande de tension ou de détente.

Certains agissent comme des « dominantes secondaires » (les « pseudo-dominantes » de différents degrés, créant avec eux de nouvelles tensions temporaires), d'autres comme des espaces de repos temporaire (créant une sensation de « presque-tonique »), etc.

C'est un peu comme dans un roman policier :

• On part en général d'une situation initiale sereine (la tonique),
• Puis survient un élément perturbateur (la dominante) qui va déclencher des péripéties,
• Enfin, viendra la résolution permettant le retour à une situation finale stable (la tonique).

Ce type de séquence est en général imbriqué sur plusieurs niveaux dans les romans, il y a des péripéties dans les péripéties (dominantes secondaires, tonalités voisines...). C'est cet enchaînement de situations stables et de tensions qui nous tient en haleine et rend le roman intéressant. Pour articuler un récit, susciter des émotions, la musique tonale est construite de manière similaire.

► L'imbrication...

"Ah ! vous dirai-je Maman", la petite mélodie vue plus haut, est un parfait exemple de ces structures "imbriquées" :

• La chanson complète, on le sait, suit le parcours Tonique → Dominante → Tonique ("tension-détente", portée du haut).
  
  
• Eh bien la première phrase suit exactement ce même parcours Tonique → Dominante → Tonique, avec suspension sur la dominante, au centre (portée du bas).

Ainsi, chaque pièce de musique tonale est une succession de cellules de forme "tension-détente", groupées en phrases de même forme, les phrases en sections, les sections en parties... jusqu'au mouvement tout entier qui adopte cette même forme. Cette autosimilarité constitue une sorte de mise en abyme (des histoires dans l'histoire).

En résumé, on peut voir la tonalité comme un système hiérarchisé (avec des degrés plus ou moins importants, puissants, ou faibles) parcouru de mouvements (enchaînements de degrés, voyageant parfois loin de la tonique), et soumis à des attractions, des tensions (la dominante) et des détentes (la tonique), créant déséquilibres et besoin d'équilibre (le retour final à la tonique).

Exemple

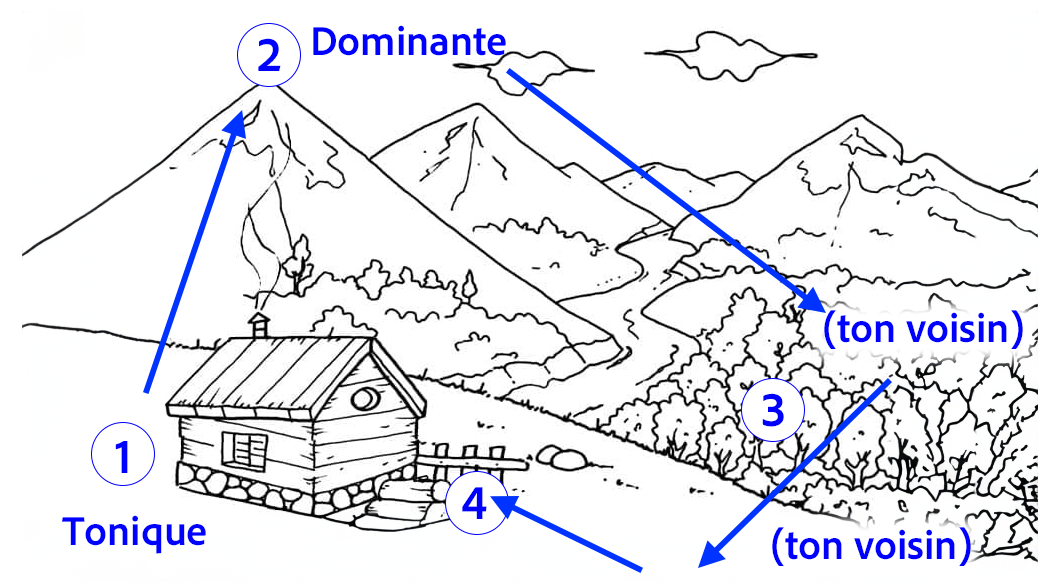
Imaginons une balade en montagne :

1. Nous partons de la maison (la tonique) ;
2. Pour atteindre directement le sommet visé (la dominante, point de tension maximale) ;
3. Au retour, puisque le temps s'y prête, nous musardons par des chemins plus éloignés (les degrés voisins) ;
4. ... Avant de rentrer finalement à la maison (la tonique).

C'est le parcours de toutes les pièces classiques.

Comme par exemple cet extrait d'un duo pour 2 violons de Maddalena Laura Lombardini Sirmen.

Dès l'écoute, on ressent instinctivement l'affirmation initiale de l'accord de Ier degré (l'accord de "tonique"), Do majeur, qui pose le cadre.

Puis, en lisant la partie de second violon (la « basse » affichée ici), on reconnaît parfaitement ce parcours : tonique-dominante-tons voisins-tonique.

Maddalena Laura Lombardini SIRMEN (1745 – 1818)

Duo pour 2 violons en Do majeur Op. 5 – Allegro final

Écouter, par Anita Mishoukova & Daniel Bell

N'oubliez pas que la première reprise est jouée...

Remarque : globablement, toute la musique moderne populaire respecte les règles de la musique tonale. En général, quand on étudie "la musique", on étudie la musique tonale...

Pourquoi ? C’est très simple : c’est une histoire de tétracordes.

Le tétracorde est un groupe de 4 notes conjointes (du latin tetrachordon = suite de 4 sons dont les 2 extrêmes forment une quatre - ou du grec « lyre à 4 cordes »).
Pythagore (il y a près de 25 siècles) est le « père de la gamme » par construction de tétracordes (voir à la fin de ce cours).

Une gamme majeure est formée de 2 « tétracordes » superposés (« inférieur » et « supérieur », une quinte plus haut).

⮕  On note la parfaite similitude entre ces 2 tétracordes : 1 ton + 1 ton + 1/2 ton.

Cette construction des gammes par tétracordes successifs peut se poursuivre en montant (vers les dièses) comme en descendant (vers les bémols) :

• En montant, chaque nouvelle gamme est à la quinte supérieure de la précédente, avec 1 # en plus
• En descendant, chaque nouvelle gamme est à la quinte inférieure de la précédente, avec 1 ♭ en plus :

Conséquence : on peut lister :

• Un « ordre des dièses » : chaque tétracorde « en montant » appelle un nouveau dièse,
• Et un « ordre des bémols » : chaque tétracorde « en descendant » appelle un nouveau bémol.

Ce n’est que par confort mnémotechnique que nous disons « le dernier dièse est la sensible » ou « l’avant dernier bémol est la tonique » ; on pourrait tout aussi bien dire, par exemple : « le denier bémol est la sous-dominante » ou « l’avant dernier dièse est la médiante », etc. (mais ce serait moins facile à retenir...)

Le plus logique serait de raisonner ainsi :

Mais cela impliquerait un chemin mental plus laborieux et moins direct…

Voici un extrait de la Suite no. 1 en Ré mineur d'Élisabeth-Claude Jacquet de la Guerre.

Toutes les formes du mineur y sont présentes tour à tour.

Élisabeth-Claude Jacquet de la Guerre (1665 - 1729)

Suite no. 1 en Ré mineur - 7. "Cannaris" (Début)

Écouter, par John Metz

Sur un mode de ré mineur sans aucun bémol à l'armure, voir l'explication dans le cours no. 4 sur les modes.